Wpływ orientacji momentu dipolowego na tendencję substancji do formowania fazy krystalicznej
Pierwsze obliczeniowe badania poświęcone procesowi krystalizacji zostały wykonane w latach 60-tych XX wieku. Z powodu ograniczonej mocy obliczeniowej ówczesnych komputerów, badane układy, tzw. ciecze proste, charakteryzowały się niezwykłą prostotą, tzn. przypominały układ cząsteczek argonu zbudowanych z pojedynczego atomu i oddziaływujących między sobą parami zgodnie z potencjałem twardych sfer (ang. hard-spheres potential) lub potencjałem Lennarda-Jones. Co ciekawe, pomimo tak znacznej prostoty badane układy relatywnie dobrze odwzorowują cechy znacznie bardziej skomplikowanych materiałów, co sprawia, że ponad 50 lat później w dalszym ciągu są one obiektem zainteresowania fizyków materii skondensowanej.[1]
Główną zaletą cieczy prostych jest fakt, iż oddziaływania pomiędzy jej cząsteczkami są precyzyjnie opisane izotropowym potencjałem co sprawia, że są układy te są idealnymi kandydatami do badań poświęconych związkowi pomiędzy potencjałem międzycząsteczkowym a makroskopowymi właściwościami układu. W tym kontekście należy wspomnieć o pracach Berthiera i Tarjusa którzy porównali strukturę i dynamikę standardowej, łatwej do przechłodzenia, mieszaniny typu Lennarda-Jonesa z jej odpowiednikiem, którego potencjał oddziaływań pozbawiony został części przyciągającej. Zauważono, że w zakresie temperatur charakteryzujących ciecze przechłodzone odziaływania przyciągające w znacznym stopniu wpływają na dynamikę systemu.[2] Kolejne badania tych systemów wykazały, że brak oddziaływań przyciągających jest bardziej odzwierciedlony w termodynamice układów niż w ich strukturze, jak również że różnice w dynamice obu systemów można rozumieć jako konsekwencje ich różnic termodynamicznych.[3] Alternatywne podejście do badanego zagadnienia zostało zaproponowane przez Coslovicha i Rolanda[4] oraz Shi i współautorów[5], którzy badali wpływ odpychania międzycząsteczkowego na dynamiczne i termodynamiczne własności binarnych mieszanin typu Koba-Andersena, które są klasycznymi modelowymi układami formującymi szkło. Autorzy zaobserwowali, że zmniejszanie wykładnika odpychającej części potencjału ma znikomy wpływ na parametr kruchości (określa on wpływ temperatury na dynamikę systemu) oraz liczbę dynamicznie skorelowanych molekuł. Należy jednak zauważyć, że po zmniejszeniu jego z 12 do 7, współczynnik dyfuzji translacyjnej wzrasta aż o dwa rzędy wielkości, a ciecze oddziałujące poprzez „miększe” potencjały pozostają dyfuzyjne w znacznie niższych temperaturach.
Przytoczone powyżej wyniki badań nad cieczami prostymi dobitnie wskazują na istnienie silnego związku pomiędzy potencjałem międzycząsteczkowym a stabilnością termodynamiczną cieczy przechłodzonych. Sugerują one, że układy charakteryzujące się słabszym przyciąganiem międzycząsteczkowym wykazują większą tendencję do krystalizacji. Wniosek też został eksperymentalnie potwierdzony poprzez wyniki otrzymane dla węglanu propylenu i 3-metylocyklopentanonu. Węglan propylenu jest dobrze znaną kanoniczną substancją formującą szkło podczas gdy 3-metylocyklopentanon wykazuje silną tendencję do krystalizacji. Różnice w stabilności termodynamicznej obu substancji są o tyle ciekawe, iż oba związki są wzajemnymi cyklicznymi analogami. Różnica w budowie obu cząsteczek jest taka, że w przypadku 3-metylocyklopentanonu dwa atomy tlenu w pięcioczłonowym pierścieniu są zastąpione przez atomy węgla. Nie wpływa to jednak znacząco na jego architekturę molekularną – kształt obu cząsteczek jest mocno zbliżony. Jedyna wyraźna różnica pomiędzy obiema molekułami widoczna jest w wartości ich momentów dipolowych. Węglan propylenu jest związkiem mocno polarnym charakteryzującym się wartością momentu dipolowego w przybliżeniu równą 5D, podczas gdy wartość momentu dipolowego znacznie mniej polarnego 3-metylocyklopentatnonu wynosi 2.9D. Różnica ta nie jest bez znaczenia w kontekście opisywanego związku pomiędzy oddziaływaniami międzycząsteczkowymi a stabilnością termodynamiczną substancji, ponieważ oddziaływania dipol-dipol są w ogólności przyciągające. Można zatem podejrzewać, że to właśnie wielkość przyciągania międzycząsteczkowego jest odpowiedzialna za znacznie większą tendencję do krystalizacji 3-metylocyklopentatnonu.
W tym miejscu należy zaznaczyć, że w przypadku molekuł rzeczywistych problem związku pomiędzy oddziaływaniami międzymolekularnymi a cechami makroskopowymi układu jest znacznie bardziej skomplikowany. Rzeczywiste molekuły zazwyczaj nie są symetryczne (w przeciwieństwie do cieczy prostych) a co za tym idzie orientacja momentu dipolowego może nie być bez znaczenia. W ramach prowadzonych badań przeprowadziliśmy szereg eksperymentów komputerowych mających na celu zbadanie wpływu wielkości jak i orientacji momentu dipolowego na stabilność termodynamiczną substancji przechłodzonych. W tym celu zaproponowano modelowy układy złożone z cząsteczek romboidalnych (RM) tzn. składających się z 4 atomów ułożonych w kształt rombu co sprawia, że odpowiednie rozłożenie ładunków elektrycznych na atomach pozwala wygenerować stały moment dipolowy o różnej orientacji – zorientowany wzdłuż dłuższej lub krótszej przekątnej rombu, co schematycznie zobrazowano na poniższym rysunku.
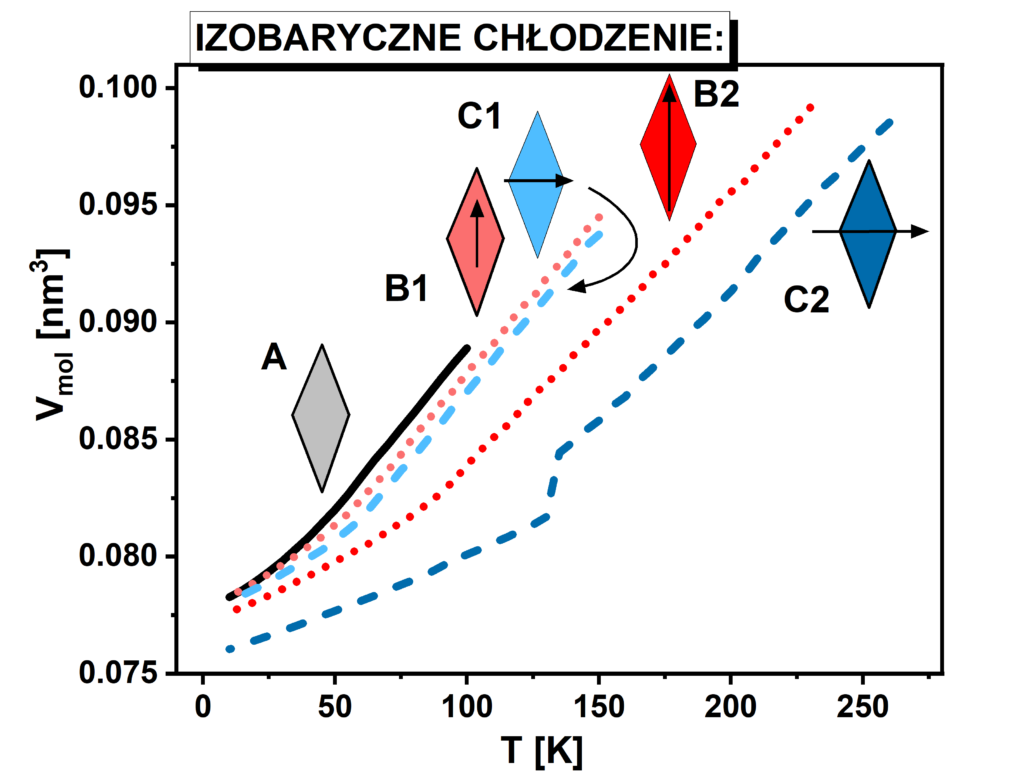
Na potrzeby eksperymentu przeprowadzono symulacje komputerowe odwzorowujące izobaryczne chłodzenie dla 5 modelowych układów. System A stworzony jest z RM bez momentu dipolowego, systemy B1 i B2 z RM posiadających mniejszy (1.61D) i większy (3.22D) moment dipolowy skierowany wzdłuż dłuższej przekątnej molekuły, podczas gdy systemy C1 i C2 analogiczne momenty dipolowe jednak zorientowane wzdłuż krótszej przekątnej molekuły. Jak widać na rysunku 1 przeprowadzone symulacje izobarycznego chłodzenia wykazały, że z pośród wszystkich badanych systemów tylko i wyłącznie jeden wykazuje skokową zmianę objętości, która świadczy o krystalizacji. Formowanie fazy krystalicznej w temperaturze 130K przez cząsteczki układu C2 potwierdzono poprzez analizę funkcji rozkładu radialnego jak również globalnego parametru porządku. Te ostanie są zaprezentowane na rysunku 2 gdzie dla układu C2 można zaobserwować ewidentny skokowy wzrost wartości globalnego parametru porządku.
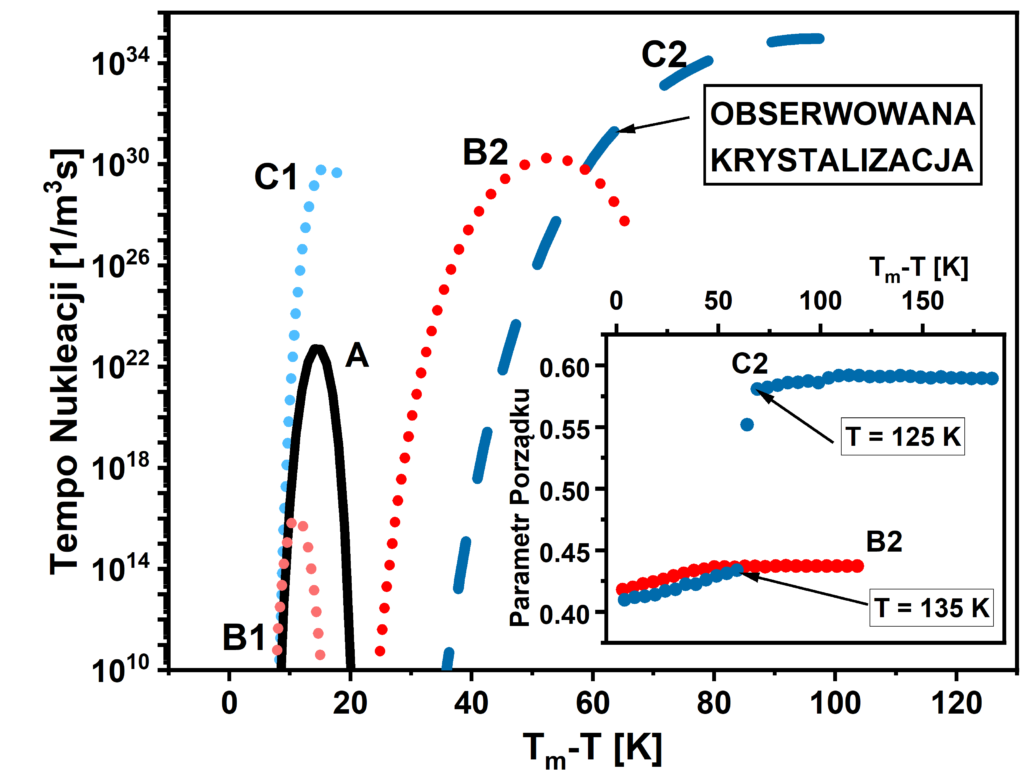
Zupełnie inne zachowanie przejawia układ B2. W tym przypadku wzrost wartości parametru porządku wynikający z ochładzania cieczy zostaje zatrzymany w pewnej temperaturze co świadczy o znacznym zahamowaniu dynamiki molekularnej i koresponduje z przejściem ciecz-szkło. Warto również zwrócić uwagę na fakt, że otrzymane wyniki mogą zostać wyjaśnione przy użyciu Klasycznej Teorii Nukleacji. Zgodnie z ogólnie akceptowanym opisem procesu krystalizacji rozpoczyna się on od powstania (w obrębie cieczy) zarodka kryształu (nukleacji), który następnie rośnie poprzez dołączanie do siebie kolejnych molekuł. Obie składowe procesu krystalizacji w racjonalny sposób opisują odpowiednio Klasyczna Teoria Nukleacji oraz model Normalnego Wzrostu Kryształu. Stworzenie zarodka wiąże się ze zmianą wartości energii swobodnej Gibbsa układu, ponieważ powstały kryształ charakteryzuje się mniejszą energią swobodną niż ciecz, z której został uformowany. Fakt ten sprzyja przemianie fazowej (jest to tzw. siła napędzająca krystalizację z ang. driving-force). Jednakże formowanie zarodka wymaga również wykonania pracy potrzebnej na stworzenie płaszczyzny oddzielającej kryształ od cieczy (interfejsu ciecz-kryształ). W konsekwencji zmiana energii swobodnej Gibbsa układu jest termodynamicznie kontrolowana przez współzawodnictwo pomiędzy siłą napędzającą krystalizację a wartością energii swobodnej interfejsu ciecz-kryształ a utworzenie stabilnego i trwałego zarodka mogącego zapoczątkować proces krystalizacji zarodka wiąże się z pokonaniem bariery energetycznej o konkretnej wartości. Nie jest to jednak jedyne ograniczenie, ponieważ przeorganizowanie molekuł prowadzące do powstania zarodka możliwe jest wyłącznie w sytuacji, gdy cząsteczki wykazują wystarczającą mobilność. Zatem w procesie zarodkowania kluczową rolę odgrywa również dyfuzja – przy dużych przechłodzeniach dynamika cząsteczek drastycznie maleje, co sprawia, że formowanie zarodków kryształów wewnątrz cieczy jest znacznie utrudnione. W konsekwencji stabilność termodynamiczna substancji zależy w pierwszej kolejności od tempa nuklecji czyli ilość stabilnych zarodków krystalicznych które mogą zostać stworzone w danej objętości substancji w konkretnym czasie. Jak można zaobserwować układ C2 charakteryzuje się największymi wartościami tempa nukleacji. Istotne jest również, że wartości tempa nukleacji, które osiąga układ C2 w temperaturze, w której krystalizuje nie są nigdy osiągane przez pozostałe modelowe układy. Zatem brak oznak krystalizacji pozostałych układów spowodowany jest niemożliwością uformowania się w nich zarodków krystalizacji.
[1] Morris J R, Dahlborg U and Calvo-Dahlborg M 2007 Recent developments and outstanding challenges in theory and modeling of liquid metals J. Non. Cryst. Solids 353 3444–53
[2] Berthier L and Tarjus G 2009 Nonperturbative effect of attractive forces in viscous liquids Phys. Rev. Lett. 103
[3] Banerjee A, Sengupta S, Sastry S and Bhattacharyya S M 2014 Role of Structure and Entropy in Determining Differences in Dynamics for Glass Formers with Different Interaction Potentials Phys. Rev. Lett. 113 225701
[4] Coslovich D and Roland C M 2011 Heterogeneous slow dynamics and the interaction potential of glass-forming liquids J. Non. Cryst. Solids 357 397–400
[5] Shi Z, Debenedetti P G, Stillinger F H and Ginart P 2011 Structure, dynamics, and thermodynamics of a family of potentials with tunable softness J. Chem. Phys. 135 084513