Wpływ oddziaływań dipol-dipol na odpowiedź dielektryczną cieczy przechłodzonych – symulacje komputerowe i badania eksperymentalne
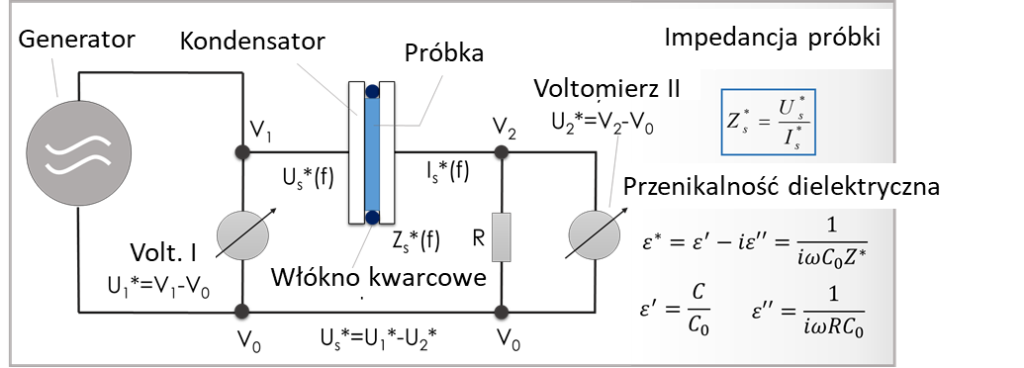
Do badania dynamiki molekularnej cieczy szkłotwórczych powszechnie wykorzystuje się metodę relaksacji dielektrycznej. Rysunek 1 wyjaśnia ideę pomiaru metodą relaksacji dielektrycznej w domenie częstotliwościowej.
Do kondensatora pomiarowego wypełnionego badanym materiałem przyłącza się z generatora napięcia sinusoidalne napięcie elektryczne o zmiennej częstotliwości, które wewnątrz kondensatora wytwarza zmienne pole elektryczne. Skutkiem przyłożonego do okładek kondensatora napięcia jest przepływ przez niego zmiennego prądu elektrycznego. Znając/mierząc zespolone wartości obu wielkości, tj.: U* i I* można w prosty sposób wyznaczyć zespoloną impedancję elektryczną badanej próbki. Z kolei zespolona impedancja elektryczna jest związana z zespoloną przenikalnością dielektryczną przy pomocy odpowiednich relacji.
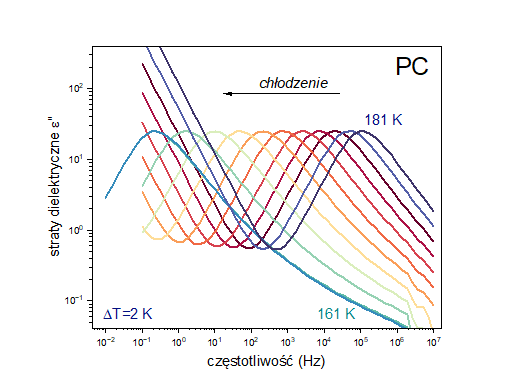
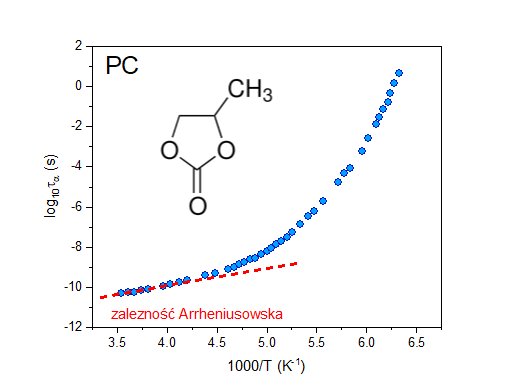
Znajomość częstotliwościowej zależności zespolonej przenikalności elektrycznej (tzw. widm dielektrycznych) jest kluczowa z punku widzenia badania zachowania dynamiki molekularnej wspomnianych już cieczy szkłotwórczych. Na rysunku 2 zaprezentowano przykładowe widma dielektryczne, które zarejestrowano dla PC w kilku różnych temperaturach. Otrzymane widma dielektryczne można między innymi wykorzystać do wyznaczenia wartości czasu relaksacji strukturalnej, który zdefiniowany jest jako odwrotność częstotliwości położenia maksimum strat dielektrycznych. Zatem możemy określić eksperymentalnie w jaki sposób dynamika strukturalna ewoluuje ze zmianą temperatury. Warto w tym miejscu dodać, że jesteśmy także w stanie badać wpływ ciśnienia na zachowanie dynamiki molekularnej. Temperaturowa zależność czasów relaksacji strukturalnej dla PC została pokazana na rysunku 3. Można zaobserwować, że czasy relaksacji strukturalnej coraz bardziej odbiegają od zależności Arrheniusowskiej wraz z obniżaniem temperatury. Taki charakter temperaturowej zależności czasów relaksacji strukturalnej określa się mianem nie-Arrheniusowskiego lub super-Arrheniusowskiego zachowania i jest to cecha charakterystyczna zachowania dynamiki strukturalnej niemal wszystkich cieczy szkłotwórczych. Drugim bardzo ważnym aspektem dotyczącym widm dielektrycznych jest kształt krzywej absorpcyjnej związanej z procesem relaksacji strukturalnej. Krzywe absorbcyjne, które zostały zarejestrowane w okolicy temperatury przejścia szklistego z reguły nie mogą być opisane prostym równaniem Debye’a – nie-Debye’owski charakter dielektrycznej funkcji odpowiedzi uznaje się za drugą charakterystyczną cechą zachowania dynamiki strukturalnej cieczy w trakcie procesu witryfikacji.
Aby opisać stopień odejścia od zachowania debayowskiego, widma dielektryczne ε* są często analizowane przy pomocy równania KWW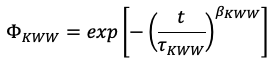 
, które wykorzystuje się do opisu kształt procesu relaksacji strukturalnej. 
.
Występujący w tym równaniu parametr βKWW, który może zmieniać się w zakresie od 1 do 0, odzwierciedla kształt widma relaksacyjnego. Jeśli jego wartość równa się jedności wówczas funkcja KWW jest tożsama z równaniem Debye’a. Natomiast, gdy maksyma absorpcyjne są szersze od procesu debye’owskiego wówczas wykładnik beta przyjmuje wartości mniejsze od jedności i jego wartość będzie maleć w miarę zwiększania się szerokości połówkowej krzywej relaksacyjnej. Analizując kształt dielektrycznych widm absorpcyjnych w okolicy temperatury zeszklenia dla około stu różnych cieczy van der walsowskich wykazano, że istnieje wyraźna korelacja między kształtem procesu relaksacji strukturalnej opisanym przy pomocy wykładnika βKWW, a wartością inkrementu dielektrycznego, który odzwierciedla polarność danej cieczy. Zgodnie ze wspomnianą korelacją dielektryczne pasma absorpcyjne odpowiadające relaksacji strukturalnej będą zwężać się wraz ze wzrostem wartości momentu dipolowego molekuły, która konstytuuje badaną ciecz. Można zaobserwować, że parametr βKWW zmienia się w zakresie od ok. 0.5 do 0.9 co w przybliżeniu odpowiada zmianie wartości dekrementu dielektrycznego w granicach od 0.1 do 220.
Istotą metody relaksacji dielektrycznej (spektroskopii dielektrycznej) jest badanie dynamiki molekularnej związanej z jednym konkretnym aspektem ruchu molekularnego, mianowicie molekularną reorientacją. Jest to możliwe wskutek oddziaływania pola elektrycznego z momentem dipolowym molekuły. Proces reorientacji molekuł można także „obserwować” przy pomocy innych metod eksperymentalnych takich jak dynamiczne rozpraszanie światła czy jądrowy rezonans magnetyczny. Obie metody są także szeroko wykorzystywane do badania procesu relaksacji strukturalnej w różnego typu cieczach szkłotwórczych. O ile obie metody dają w zasadzie spójne wyniki z wynikami z pomiarów dielektrycznych w zakresie temperaturowych charakterystyk czasów relaksacji strukturalnej, to w przypadku zachowania kształtu funkcji odpowiedzi zauważono duże rozbieżności. Zarówno widma uzyskane z pomiarów DLS jak i NMR mają quasi uniwersalny charakter. To znaczy, że funkcje odpowiedzi związane z procesem relaksacji strukturalnej dla różnych typów cieczy mają praktycznie ten sam kształt. Na podstawie analizy tych widma przy pomocy funkcji KWW wykazano, że wykładnik βKWW przyjmuje praktycznie stałą wartość, która wynosi ok. 0.5. Zatem kształt widm pochodzących z pomiarów DLS i NMR może różnić się znacząco od tych zarejestrowanych przy pomocy spektroskopii dielektrycznej. Wspomniana rozbieżność pogłębia się ze wzrostem polarności danej substancji, ponieważ jak już wcześniej zauważono, widma dielektryczne bardzo polarnych cieczy mają prawie debye’owski kształt. Natomiast te rozbieżności nie występują w przypadku bardzo słabo polarnych cieczy.
Na podstawie wyników analizy porównawczej widm zmierzonych przy pomocy trzech komplementarnych technik badawczych (BDS, DLS i NMR), które wszystkie śledzą reorientacje molekuł, wyłania się bardzo ważne pytanie: Dlaczego kształt widm dielektrycznych reprezentujących proces relaksacji strukturalnej zmienia się tak silnie ze zmianą polarności badanej substancji?
Punktem wyjścia do rozwiązania tego problemu jest analiza funkcji korelacji makroskopowego momentu dipolowego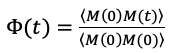 
, która wiąże się z zespoloną przenikalność elektryczną poprzez transformatę Laplace’a 
.
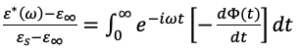Biorąc pod uwagę, że makroskopowy moment dipolowy wyraża się przez sumę wszystkich momentów dipolowych molekuł, funkcję Φ(t) możemy zapisać w następującej formie: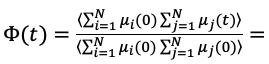 
.
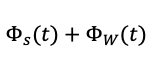Pierwszy człon w powyżej sumie reprezentuje funkcję korelacji własnej (ang. self-correlation function) natomiast drugi człon to funkcja korelacji wzajemnej (ang. cross-correlation function). Bardzo często wyrażano przekonanie, że dla prostych cieczy van der Waalsowskich nie występują żadne korelacje wzajemne i dlatego drugi człon może być pominięty, tzn. ΦW(t)⁓0. Zgodnie tym przekonaniem należałoby oczekiwać, że wszystkie widma dielektryczne cieczy typu van der Waals powinny odzwierciedlać wyłącznie funkcję korelacji własnej.
Istnieją jednak pewne przesłanki, że w przypadku cieczy polarnych nie można pominąć wkładu związanego z korelacjami wzajemnymi. Co więcej oczekuje się, że wkład korelacji wzajemnych będzie
dominujący dla bardzo polarnych układów. Niestety nie sposób udowodnić tej hipotezy bezpośrednio na podstawie pomiarów dielektrycznych, ponieważ metoda relaksacji dielektrycznej nie pozwala mierzyć tych wkładów odrębnie. Jest to jednak możliwe wykonując symulacje komputerowe dynamiki molekularnej, co zostało opisane w naszej publikacji, która ukazała się w Physical Review Letters.
Symulacje komputerowe wykonano dla quasi-rzeczywistych molekuł, które składały się z czterech atomów węgla połączonych w ten sposób, że tworzyły strukturę rombu, tak jak to pokazano na rysunku 4.
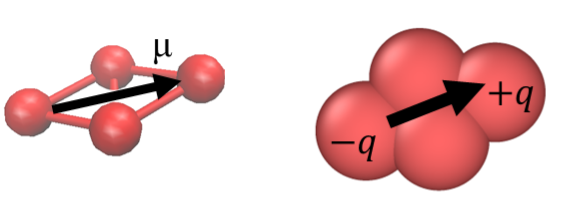
Ponieważ w eksperymencie symulacyjnym badano zjawisko zaniku wektora polaryzacji P(t)=M(t)/V próbki po wyłączeniu zewnętrznego stałego pola elektrycznego E, dlatego nasze molekuły były obdarzone trwałym momentem dipolowym μ. Aby zbadać wpływ wartości momentu dipolowego na odpowiedź dielektryczną, przeprowadzono symulacje dla cząsteczek słabo (μ=0.4D) i mocno polarnych (μ=4D). W rezultacie otrzymano pełną zgodność z obserwacjami eksperymentalnymi. To znaczy, że ze wzrostem polarności kształt funkcji odpowiedzi dielektrycznej zmienia się w stronę bardziej eksponencjalnej (debye’owskiej) zależności. Zgodnie z rysunkiem 5, dla molekuł słabo polarnych wykładnik βKWW wynosi 0.7, podczas gdy dla mocno polarnych βKWW =0.93.
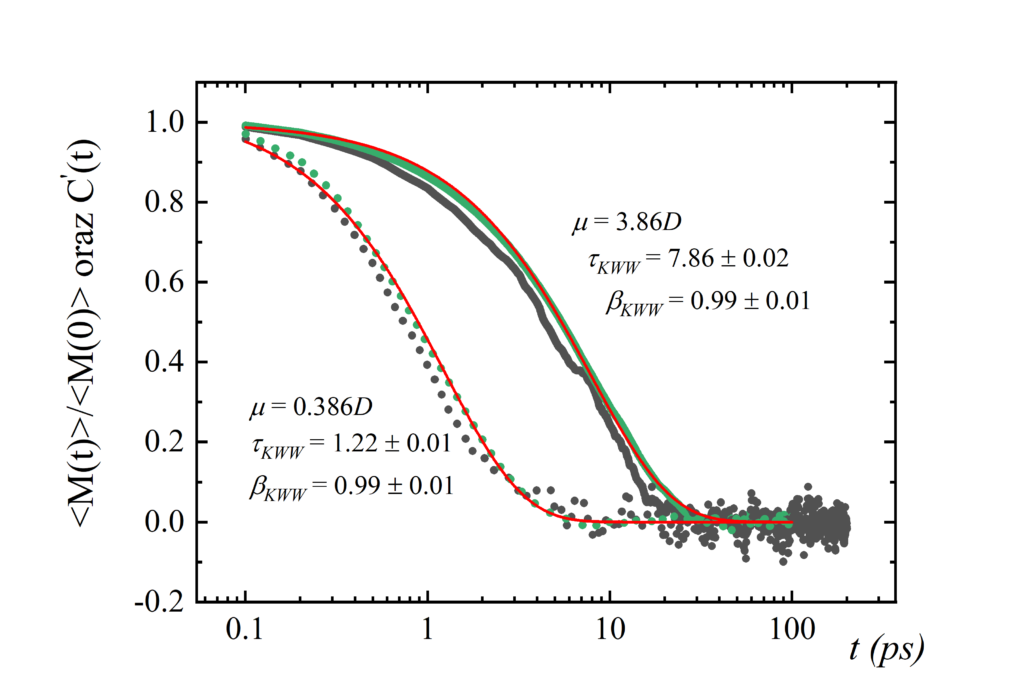
Jednakże najważniejszym wynikiem, który uzyskano z symulacji komputerowych było udowodnienie, że w przypadku słabo polarnych molekuł kształt funkcji odpowiedzi dielektrycznej jest w zasadzie tożsamy z funkcją korelacji własnej, podczas gdy dla mocno polarnych molekuł funkcja odpowiedzi dielektrycznej zdominowana jest przez wkład od korelacji wzajemnych. Ponadto wykazano, że funkcja korelacji własnych zanika szybciej aniżeli funkcja korelacji wzajemnych. Uzyskanie tych niezwykle ważnych wyników było możliwe wyłącznie dlatego, że w przypadku symulacji komputerowych można odrębnie wyznaczyć (wyliczyć) oba człony występujące w równaniu .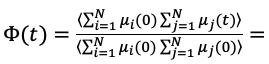
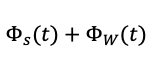Zatem widmo dielektryczne cieczy polarnych zmierzone eksperymentalnie w domenie częstotliwościowej, które odzwierciedla proces reorientacji całej molekuły (tzw. relaksacja strukturalna) można w ogólności traktować jako złożenie dwóch modów: wolniejszego związanego z korelacjami wzajemnymi w badanym układzie i szybszego opisującego korelacje własne. Takie zachowanie schematycznie zilustrowano na rysunku 6.
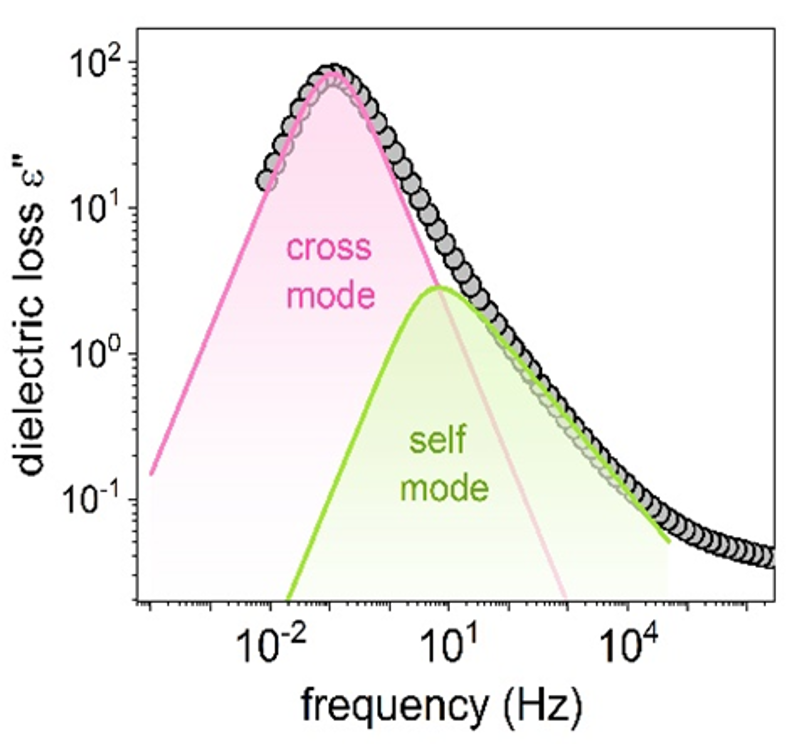
Istnienie obu modów charakteryzujących się różnymi skalami czasowymi, zostało także potwierdzone eksperymentalnie wykonując eksperyment starzeniowy opisany szczegółowo w innej pracy, która ukazała się w Journal of Chemical Physics Letter. Ideą tego eksperymentu było wykazanie, zakładając wolniejszy zanik funkcji korelacji wzajemnej niż własnej, że nie można opisać przy pomocy pojedynczej funkcji KWW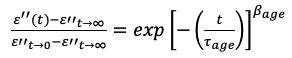 
zmierzonej eksperymentalnie czasowej zależności strat dielektrycznych ε’’ dla wybranej częstotliwości pola mierzącego poniżej temperatury zeszklenia. Natomiast oczekiwano, że powinna stanowić superpozycję dwóch takich funkcji
. Takiego zachowania naturalnie należy spodziewać się tylko w przypadku pomiarów cieczy mocno polarnych, co potwierdzają wyniki uzyskane dla fluorowanej pochodnej PC (FCP) i pokazane na rysunku 7.
Opis czasowej zależności strat dielektrycznych zmierzonej w eksperymencie starzeniowym przy pomocy pojedynczej funkcji KWW jest w zupełności wystarczający, jeśli dotyczy słabo polarnych molekuł. Tak rzeczywiście jest na przykład w przypadku karwedilolu (patrz rysunek 8)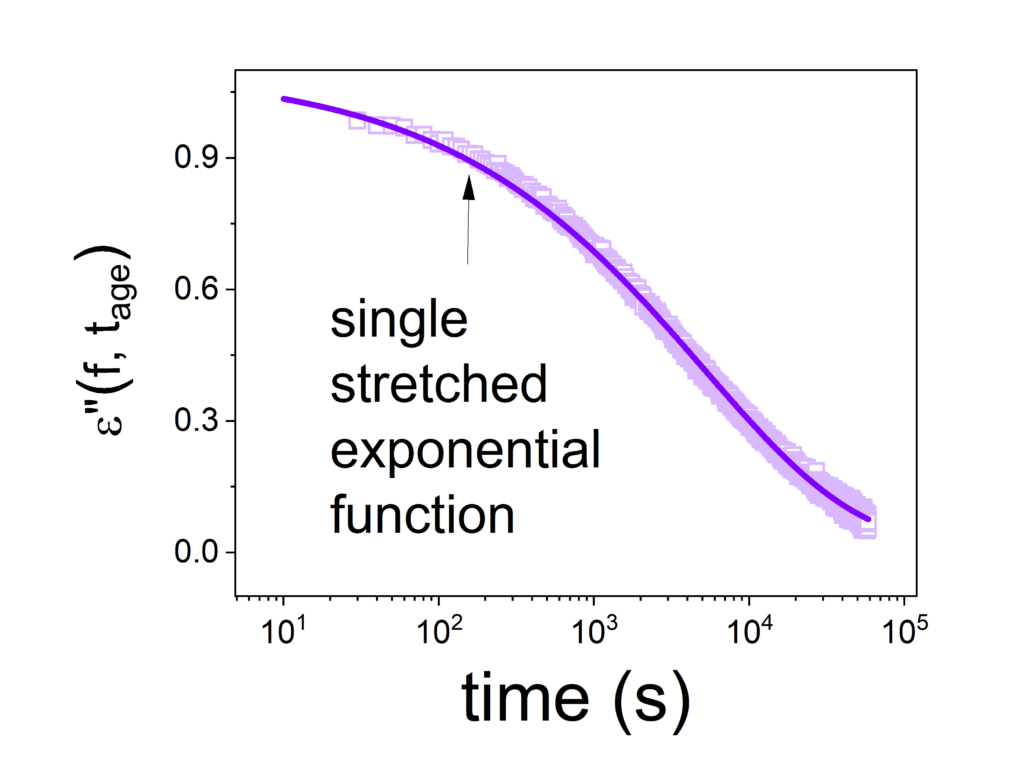
Jako podsumowanie należy stwierdzić, że na podstawie symulacji komputerowych dynamiki molekularnej wykazaliśmy, że dla polarnych cieczy nie można pominąć wkładu do funkcji relaksacji dielektrycznej pochodzących od korelacji wzajemnych. Co więcej udowodniono, że dla silnie polarnych układów ten wkład staje się dominujący. Ponadto koncepcja, że odpowiedź dielektryczna polarnych cieczy zawiera dwa wkłady: wolniejszy związany z korelacjami wzajemnymi oraz szybszy zależny od korelacji własnych została także pośrednio udowodniona na podstawie dielektrycznego eksperymentu starzeniowego.